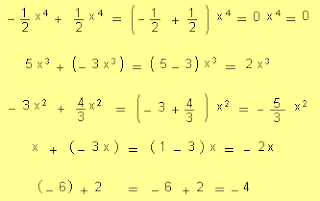6.- Video Propiedades de la Multiplicación de Polinomios

Dictado por: Yusnery Urdaneta 

5.- Video Sustracción de Polinomios

Dictado por : Bellaly Urrutia 

4.- Video Adiciòn de Expresiones Polinómicas

Dictado por: Yaqueline Cadenas

3.-Video Clasificacion de un Polinomio

Dictado por: Rosiner Villarreal

2.-Video Elementos de un Polinomio

Dictado por: Omer Hernandez

1.-Video Función polinómica

Dictado por: Omer Hernandez

6.3.1- Propiedades de la Multiplicacion de Polinomios

 Propiedad conmutativa: dado dos polinomios cuales quiera P(x) y Q(x) sobre Q se cumple que: P(x).Q(x)= Q(x).P(x)

 Propiedad asociativa: dado tres polinomios cualesquiera P(x), Q(x) y R(x) sobre Q se cumple que: [P(x).Q(x)].R(x)= P(x). [Q(x) .R(x)]
 Existencia de elemento neutro: para todo polinomio Q(x) sobre Q, existe el polinomio unidad P(x)=1 tal que: 1=1.Q(x)= Q(x).
 Propiedad distributiva:de la multiplicación con respecto a la adición dado tres polinomios P(x), Q(x) y R(x) sobre Q(x) la Propiedad distributiva establece que P(x)+ [Q(x) +R(x)]= P(x).Q(x)= Q(x).R(x)

http://www.monografias.com/trabajos16/productos-notables/productos-notables.shtml

6.3- Productos de Polinomios

Se procede de la siguiente manera:

 Se ordenan (si no están ordenados) los polinomios en forma decreciente o creciente
 Se multiplica cada termino de un polinomio por el segundo polinomio
 Se efectúan los productos entre los monomios
 Se suman los términos semejantes.


Ejemplo: tendremos dos Polinomios Q(x) y P(x)

Resolucion:

Ejemplo: Dados los Polinomios P(x) Y Q(x) se multiplica:

Otra manera de resolverlo seria así:

http://www.google.co.ve/search?sourceid=navclient&aq=0&oq=productos+de+poli&hl=es&ie=UTF-8&rlz=1T4GZHZ_es___VE393&q=productos+de+polinomios

6.2- Producto de un Monomio por un Polinomio

• Para efectuar el producto de un monomio por un polinomio se multiplica el monomio por cado uno de los términos del polinomio por ejemplo el siguiente producto:

• (-5X³) . (2X⁴-X³+7X²-3X)
• (-5X³).(2X⁴)+(-5X³).(-X³)+(-5X³).(7X²)+(-5X³).(-3X)= -10X⁷+5X⁶-35X⁵+15X⁴
• En general se toma en cuenta los siguientes pasos:


• Se ordena el polinomio de forma decreciente o creciente.

• Se aplica la propiedad distributiva del producto; si así lo prefiere.


• Se efectúa la operación de producto entre el monomio y polinomio.


• Otra manera de resolver un producto de un monomio por un polinomio es escribiendo el monomio debajo del polinomio y se efectúa la operación de producto.
• Por ejemplo: (-2X³). (3X-X⁶+X²+8); primero se ordena el polinomio en este caso de manera decreciente


• a) -X⁶+X²+3X+8

-2X³
_ ____________
2X⁹-2X⁵-6X⁴-16X³

b) -2/5X⁶-4X⁴-3/2X²+5X
     1/3X²
______________________
  -2/15X⁸-4/3X⁶-1/2X⁴+5/3X³

http://espanol.answers.yahoo.com/question/index?qid=20090109120648AAF92kD

6.1- Productos de Monomios

• Monomio: es una expresión algebraica n la que se utiliza letras, números y signos de operaciones.

Las únicas operaciones q aparecen entre las letras son el producto y la potencia de exponentes natural. Se denomina polinomio a la suma de varios monomios.

Un monomio es un polinomio con un único término.


• Elemento de un monomio:

Posee una serie de elementos con denominación específica:

• Por ejemplo: Dado el monomio 5X³ se distinguen los siguientes elementos:

• Signo = ₊

• Coeficiente = 5

• Parte literal = X³



• Para multiplicar dos monomios, se multiplican los coeficientes y las potencias que tiene igual base; recordemos que para multiplicar por potencia de igual base, se coloca la misma base y se suman los exponentes.

• Por ejemplo=

• Para multiplicar (3X⁸)×(-2X³)= Se procede así:

• Se multiplican los coeficientes 3 y -2, es decir , (3)×(-2) =-6

• Se multiplican las potencias de X= X⁸.X³ = X¹

• Luego decimos : (3X⁸).(-2X³) = -6X¹¹



• Dado los monomios; (6X³).(-4X⁵)=(6.(-4)).(X³.X⁵)= -24X⁸

• (-6X³).(-3X⁴).(X¹⁰)=((-6).(-3).1).(X³.X⁴.X¹⁰)= -18X¹⁷

• (7/2X⁵).(10/7X⁹)=(7/2 . 10/7).(X⁵.X⁹)=70/14X¹⁴=35/7X¹⁴=5X¹⁴

• Otro tipo de monomio es el que está formado por su parte literal por potencias de base diferentes; el producto de este tipo de monomio se efectúa de manera similar: se multiplican primero los coeficientes y luego se multiplican las potencias que tienen igual base entre si.

• Ejemplos:
• 3XY².5X²Y = (3.5).(X.X²).(Y².Y)= 15X³Y³
• 4X². 8X³Y = (4.8). (X².x³). (Y) =32X⁵Y
• (5a²b³).(-3ab). (4b²) = (5.(-3).4).(a².a).(b³.b.b²)= -60 a³b⁶

• (3/4X²Y³).(2/3 XY).(6/5X⁵) =(3/4.2/3.6/5).(X².X.X⁵).(Y³.Y)=3/5X⁸Y⁴




http://www.google.co.ve/search?sourceid=navclient&hl=es&ie=UTF8&rlz

6.- Multiplicación de Polinomios

Multiplicación de una Constante por un Polinomio
Para multiplicar una constante por un polinomio, se multiplica el coeficiente de cada término del polinomio por la constante K.

Dado una constante K y un

Ejemplo: tendremos un K que tendra valor igual a 5 por un polinomio P(x)

x  (5)

Ejemplo: tendremos un K que tendra valor a 3 por un polinomio Q(x)

Q(x) =

 

http://es.wikipedia.org/wiki/Polinomio

5.- Sustracción de Polinomios

Para restar dos polinomios se suma al minuendo el opuesto del sutraendo, es decir, se cambia el signo a todos los términos del segundo polinomio (sustraendo) y se suman los resultados.Para restar el polinomio Q(x) del polinomio P(x) se debe sumar a P(x) el polinomio opuesto de Q(x).


P(x) - Q(x) = P(x) + [ - Q(x)].

Ejemplo de este seria:

http://www.cnice.mecd.es/Descartes/Bach_CNST_1/Polinomios/polinom1.htm#suma

4.1- Propiedades de la Adición de Polinomios

 Propiedad conmutativa: se cumple P(x)+Q(x)= Q(x)+P(x)



 Propiedad asociativa: se cumple [P(x)+Q(x)]+R(x)= P(x)+ [Q(x) +R(x)]


 Existencia de elemento neutro: 0(x)= 0xn +xn+1+0x+0=0 tal que P(x)+0(x)= P(x)


 Existencia del elemento opuesto: P(x)+[(-P(x)]=0


http://www.ejercitando.com.ar/teormate/suma%20de%20polinomios.htm

4.- Adición de Polinomios

Adición de expresiones polinómicas:

    Para sumar expresiones polinomicas de dos o mas números se suman los términos, que son semejantes entre si, lo cual equivale a sumar unidades con unidades, decena con decenas, centenas con centenas, etc.

Ejemplo:  5639 esto podria descomponerse de la siguiente manera
                 5639 : 5 . 1000 + 6 . 100 + 3 . 10 + 9 .1

Adición de Polinomios:

Definición: Sea 

Dados dos polinomios A(x) y B(x), se llama suma o adición a otro polinomio S(x) cuyos términos son la suma de los términos de igual grado de los polinomios sumandos.

Ejemplo 1:

Dados los polinomios 

Hallar S(x) = A(x) + B(x)

Una manera práctica de resolución es disponer los polinomios ordenados, encolumnando los monomios de igual grado 

Como cada término de la suma S(x) se obtiene sumando los coeficientes de los monomios de igual grado, se puede escribir que:

 
 

     

por lo tanto queda :     
 

Otra forma de resolver es



 S(x) = A(x) + B(x) =

Se eliminan los parentesis y queda de la siguiente manera:

 

 operando con los coeficientes, se obtiene

 
http://es.wikipedia.org/wiki/Polinomio

3.- Clasificación de los Polinomios

Algunos polinomios reciben un nombre en especial según el número de términos no semejantes:

          Monomio: es el polinomio que esta formado por un solo termino

Ej: P(x)= Ej: Q(x)=

                    

           Binomio: es un polinomio formado por dos términos ,

Ej: P(x)=

           Trinomio: es un polinomio formado por tres términos;

Ej:P(x)=

http://www.vitutor.com/ab/p/poli_20.html

                                   

2.1.- Elementos de un Polinomios

Coeficiente de un polinomio

Dado el siguiente polinomio  

5y⁴  - 2y³ + y² - 7y + 8 , donde 5, 2, 1, 8 son números racionales, y se denominan coeficientes del polinomio.

http://ponce.inter.edu/cremc/polinomio1.htm

Función de un polinomio  

Cada uno de los sumandos de el polinomio p(x) = con sus respectivas variables se denominan función de polinomio.

Términos de un polinomio

Es una expresión que esta formada por un coeficiente y una variable,  y está separados por los signos de suma o resta.

Ejemplo:   3x , -2x², 4

  

http://ponce.inter.edu/cremc/polinomio1.htm

Grado de un polinomio 

Es el mayor exponente con el que aparece la variable, ( x, y, z...) con coeficiente no nulo.

Ejemplo: 

x² + 2x - 8

es decir que los grados del polinomio son: 2, 1, 0

  

Términos semejantes de un polinomio

Dos términos de un polinomio se dicen semejantes si tiene la misma variable y el mismo grado.

Ejemplo:

6a²b es semejante con -8 a²b  porque tienen la misma variable y el mismo grado


http://www.geolay.com/pagehtm/algeb01.htm#34

2.-Función Polinómica

    

El estudio de las situaciones de la vida real invulocran a menudo una función. La palabra función expresa la idea de la dependencia entre dos variables. Dado el valor de la variable independiente, queda determinado el valor de la otra. Si se conoce el valor de una variable, se puede hallar el valor de la otra por medio de una función.

De forma general definimos una función polinómica:

                   

 Es decir que una función polinómica no es más que una expresión acompañada por una variable o varias variables que representan un numero racional cualquiera.

   Para que una función sea polinómica, los exponentes de la funcion deben ser todos enteros positivos, o cero. Si hay exponentes fraccionarios o negativos, ya no se trata de una función polinómica. 

                   Ejemplo:

Función Polinómica

No es una  Función Polinómica

http://es.wikipedia.org/wiki/Funci%C3%B3n_polin%C3%B3mica

1.-Objetivo General

• Identificar los Polinomios y sus Operaciones utilizando diferentes técnicas .

Introducción

 Hace unos 4.000 años, los babilonios conocían la manera de encontrar la solución positiva de ciertos tipos de ecuaciones. 

Babilonios

Más adelante, matemáticos griegos, hindúes, árabes y europeos se dedicaron al estudio de estas ecuaciones y lograron avanzar a través del tiempo, hasta encontrar asi la fórmula para resolver cualquier ecuación. Dichas ecuaciones son conocidas como funciones polinómicas, un ejemplo claro es

  

  

http://www.rena.edu.ve/TerceraEtapa/Matematica/tema32web/Polinomios.html